This is the group project of SDSC4107 – Financial Engineering and Analytics. I did the project in my year 3 2022/23 Semester B.
Presentation Slides:
Course Instructor: Dr. Qi WU
Introduction
This report focuses on the topic of “Stock market price trend prediction using time series forecasting.”, which we focus on three major models, including autoregressive integrated moving average model (ARIMA), Long-Short-Term Memory model(LSTM) and Multi-layer model (MLP). The dataset used for this analysis is the Hang Seng Index (HSI) from the years 2010 to 2023. The dataset is loaded into Python, and libraries are imported for data manipulation, visualization, and modeling.
Although the HSI is a widely used yardstick for measuring the performance of the Hong Kong stock market, predicting its future values can offer important clues about the state of the economy. Time series forecasting can assist traders and investors in deciding whether to buy or sell stocks in a way that will maximize portfolio returns. Forecasting can also be used to spot developing trends and market patterns, which helps financial analysts predict how the markets will behave in the future. By analyzing historical trends and identifying patterns, forecasting can assist in predicting future values, which can help to inform investment strategies and reduce risk.
Forecasting can also give important insights into the underlying elements that influence the performance of the stock market, such as monetary indicators, political developments, and investor sentiment. Therefore, in this report, we try to analyze the performance of three different commonly used models, including ARIMA, LSTM and MLP, on HSI and examine the result using different measures.
Time series forecasting on the HSI can offer insightful information about the stock market’s potential performance, helping investors make more accurate predictions about the future, make wise investment decisions and reduce investment risk. We therefore hope that our findings in this report can provide insight into each model’s market performance, the benefits of various time series forecasting models, and their application in practice.
Methodology
Model 1: Autoregressive Integrated Moving Average
The Autoregressive Integrated Moving Average (ARIMA) model is a popular linear time series forecasting model that combines autoregressive (AR) and moving average (MA) components with differencing to make the time series stationary. It is particularly suitable for univariate time series data with no obvious seasonal components.
To forecast HSI prices using the ARIMA model, the following steps were carried out:
Data Acquisition and Preprocessing: The historical HSI data was obtained from Yahoo Finance using the yfinance library. The dataset was resampled to averages every month and split into two sets, one for training (80% of the data) and another for testing (20% of the data).
Splitting the dataset: The dataset is divided between training and testing sets, with the latest 30 months of data saved for testing.
Model Selection: The auto_arima function from the pmdarima library was used to find the best-fitting ARIMA model based on the Akaike Information Criterion (AIC). The function performs a stepwise search for the optimal model, considering various combinations of p, d, and q parameters.
Performing stepwise search to minimize aic ARIMA(0,2,0)(0,0,0)[0] intercept : AIC=322.554, Time=0.02 sec ARIMA(1,2,0)(0,0,0)[0] intercept : AIC=322.988, Time=0.03 sec ARIMA(0,2,1)(0,0,0)[0] intercept : AIC=323.177, Time=0.21 sec ARIMA(0,2,0)(0,0,0)[0] : AIC=320.573, Time=0.04 sec ARIMA(1,2,1)(0,0,0)[0] intercept : AIC=324.773, Time=0.19 sec
Best model: ARIMA(0,2,0)(0,0,0)[0]
Total fit time: 0.519 seconds

Figure 1. ARIMA model summary
Model Diagnostics: Once the optimal ARIMA model is selected, we perform diagnostic checks by plotting the residuals and analyzing their properties. This step ensures the model’s assumptions are not violated, and its performance is reliable.

Figure 2. ARIMA Model Diagnosis Diagram
Model Evaluation: The ARIMA model is applied to the test dataset to forecast future HSI closing prices. We then evaluate the model’s accuracy by comparing its predictions to the actual HSI prices using performance metrics such as Root Mean Squared Error (RMSE) and Mean Absolute Percentage Error (MAPE).
Model 2: Long Short-Term Memory Networks
LSTM is a type of Recurrent Neural Network (RNN) architecture that is particularly well-suited for handling time-series data. LSTM networks are designed to handle long-term dependencies, which makes them well-suited for time-series data where the order of events matters.

Figure 3. LSTM Model Summary The LSTM model used in this report consists of several layers:
-Input layer: The input layer receives the input data, which in this case is the historical stock market prices.
-LSTM layer: The LSTM layer is the core of the model. It consists of several memory cells, which allow the network to capture long-term dependencies in the data. Each memory cell has three gates: the input gate, forget gate, and output gate. These gates control the flow of information in and out of the memory cell.
-Dense layer: The dense layer is a fully connected layer that maps the output of the LSTM layer to the output of the model.
-Dropout layer: The dropout layer is used to prevent overfitting. It randomly drops out some of the neurons in the network during training, which helps to prevent the network from memorizing the training data.
The LSTM model is trained using backpropagation through time (BPTT), which is a variant of the backpropagation algorithm that is designed for recurrent neural networks. During training, the model is presented with a sequence of historical stock market prices and asked to predict the next value in the sequence. The difference between the predicted value and the actual value is used to update the weights in the network, using gradient descent.
It is also trained using the Adam optimizer, which is a popular optimization algorithm for training neural networks. The optimizer adjusts the learning rate during training, which helps to improve convergence.

Figure 4. Preprocessing HSI dataset
The data is pre-processed by checking for null values using the isnull() function and dropping the rows containing null values using the dropna() function.
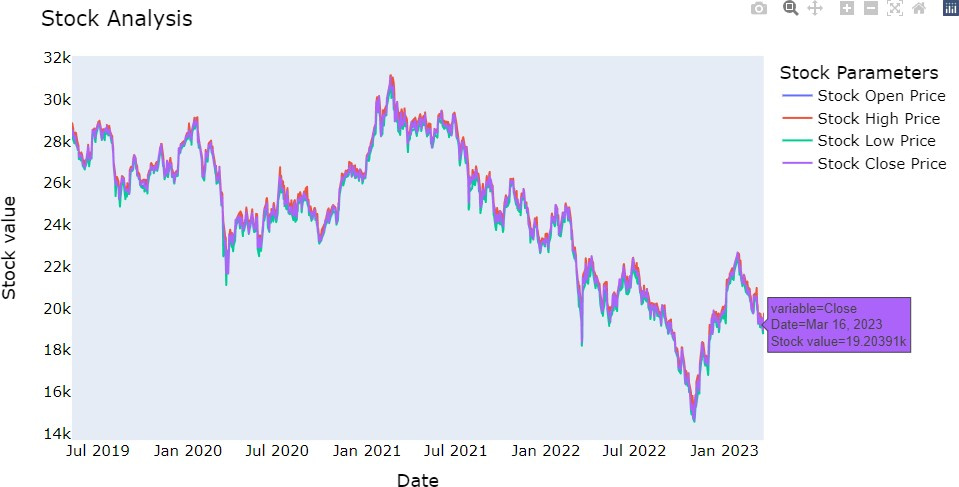
Figure 5. HSI stock analysis
A time series plot is created to visualize the data. The plot shows the trend of the HSI over time, indicating a general downward trend with some fluctuations.
The LSTM model is used for time series forecasting. The data is split into training and testing sets. The MinMaxScaler function is used for feature scaling. The LSTM model is trained on the training set using a sequential model with dense and dropout layers. The model is then evaluated on the testing set using the mean squared error (MSE) and mean absolute error (MAE) metrics.
Model 3: Multi-layer Perceptron
The mechanism of MLP(Multi-Layer Perceptron): MLP model is a type of feedforward neural network that consists of multiple layers of artificial neurons and organized in a sequence. Each neuron in the network receives input from the previous
layer and passes output to the next layer until the final output layer produces the predicted result.
The MLP model is a supervised learning algorithm that is commonly used for regression and classification tasks, including image and speech recognition, natural language processing, and most importantly, financial forecasting. It is a powerful tool for capturing complex nonlinear relationships between inputs and outputs, making it particularly useful in applications where traditional linear models may not be sufficient. Therefore in this project, we use it as a tool to forecast the HSI.
Before performing MLP, as we only obtain numeric data from the dataset, we set the “closing price” as our target attribute, and there are in total 2518 input parameters for training the model. The following are the null values in the dataset.

Figure 6. Dataset Null value
After dropping the null value, we started to construct our model. It is constructed of 3 dense layers, and 2 dropout layers. While the dense layer is a layer that is deeply connected with its preceding layer which means it maps all the output of its previous layer and used to change the dimension of the vectors using every neuron. In the model, the first two 2 RELU functions and the last one are linear as to give weight to the remaining 65 parameters. For the dropout layer, it is used to prevent overfitting. By randomly dropping out some neurons from the previous layer, the influence of the training data can be minimized.

Figure 7. MLP Model Summary
The dataset is split into two sets, one for training (67% of the data) and another for testing (33% of the data). We set the step-back function in the model to be in 3 days, which means each prediction is 3 days after the training days, each day is predicted using the sum of its previous record to estimate the result, which below is the graph of the prediction we draw from the model.

Figure 8. MLP Model prediction
Multilayer Perceptron improved from the simple perceptron model which can only work with one neuron and understand linear relationship between input and output, with MLP, the horizons are expanded and now can have many layers of neurons, and are capable of learning more complex patterns.
Result and Discussion
Model 1: Autoregressive Integrated Moving Average
After implementing the ARIMA model, the ‘auto_arima’ function identified the best model as ARIMA(0,2,0), based on the lowest AIC value. The diagnostic plots indicated that the model’s residuals were approximately normally distributed with no apparent autocorrelation, suggesting the model is a good fit for the data.
Upon applying the ARIMA model to the test dataset, we generated a time series plot that displayed the actual HSI prices, the predicted prices, and the corresponding 95% confidence intervals. The visual inspection of the plot reveals that the ARIMA model captures the overall trend of the HSI, although it may not precisely predict the short-term fluctuations.
Prediction Result:

Figure 9. ARIMA Prediction Result
To further assess the model’s performance, we computed the RMSE and MAPE values. The RMSE value was found to be 2718.10, while the MAPE value was 11.97%. These metrics show that the ARIMA model provides a reasonably accurate forecast of the HSI closing p
In this report, we applied the ARIMA model to forecast HSI prices and assessed its performance using the RMSE and MAPE metrics. The results show that the ARIMA model is capable of capturing the general trend of the HSI prices, but further improvements could be made by incorporating additional factors or using more advanced time-series models, such as LSTM or MLP. Overall, the ARIMA model can serve as a useful tool for HSI price prediction when used in combination with other analysis methods.
Model 2: Long Short-Term Memory Networks

Figure 10. LSTM model prediction results
In this report, the LSTM model is trained on a training set of historical stock market prices, and the performance of the model is evaluated on a testing set. The mean squared error (MSE) and mean absolute error (MAE) are used as evaluation metrics. These metrics quantify the difference between the predicted values and the actual values, with lower values indicating better performance.

Figure 11. MSE, MAE and Root MSE results
The mean squared error (MSE) and mean absolute error (MAE) for the testing set are calculated as 997566.67 and 826.06, respectively. The model performs not bad, it somehow captures the overall trend of HSI which is indicating that the LSTM model can also be used for time series forecasting of stock market prices.

Figure 12. Plotting simple HSI trend
The time series plot shows that the HSI has experienced an overall downward trend with some fluctuations. The fluctuations in the HSI can be attributed to various factors, such as changes in economic policies, geopolitical tensions, and natural disasters.
Overall, this report shows that time series forecasting using LSTM models can be an effective method for predicting stock market prices. It is important to note that other factors beyond time series data can also influence stock market prices, and therefore, predictions made using time series models should be used in conjunction with other analysis methods.
Compared to other machine learning models like MLP (Multi-Layer Perceptron) or ARIMA (AutoRegressive Integrated Moving Average), LSTM models are generally better suited for time-series forecasting tasks because:
They can handle variable-length input sequences: In time-series forecasting, the length of the input sequence (i.e., the historical data) can vary depending on the forecasting horizon. LSTM models can handle variable-length input sequences, making them more flexible than models that require a fixed-length input.
They can capture long-term dependencies: Time-series data often involves complex dependencies between past and future values. LSTM models are designed to capture these dependencies, making them more effective at modeling complex patterns in the data.
They can handle nonlinear relationships: Time-series data often involves non-linear relationships between past and future values. LSTM models are capable of modeling these non-linear relationships, making them more effective than linear models like ARIMA.
Model 3: Multi-layer Perceptron
For the prediction result, after testing, we find that the model perform best with 200 epochs with batch size of 2, which means the algorithm takes the first 2 samples from the training dataset each time to trains the network and take the next two, which is the third and the fourth in training the network again, so it is relatively computational expensive. The following are the result,

Figure 13. Plotting MLP model prediction trend
With the loss of 14092188 when entering the epoch 200, as the number shows, both the training and testing MSE lie in a stable range, which is around 2500 RMSE. Besides, from the graph, it can be seen that the prediction on the both the training and the testing set is lower than the true index, it may due to the initiate point of the weighting parameter is from zero, and with the 2 drop-out function in the model, the overfit problem is solved, but also result in the low training and testing score. The model takes 413 seconds in computing, which is expensive as it is in batch size of 2.
Lastly, as the graph shows, the prediction has the RMSE of 2677 even in predicting the 3 days result. It can be clearly shown that there are still a lot of adjustments that need to be made if we want to make profit using the MLP model in predicting the actual market stock price.
Limitations and Future Studies
Limitation
Despite the promising results obtained by the three models we built in this report, there are still some limitations that need to be acknowledged. One of the main limitations is the assumption that the future behavior of the HSI index will follow the patterns observed in the past data. However, the financial market is notoriously unpredictable, and it is important to take into account all external factors when making predictions based on time-series data.
Another limitation is the reliance on a single indicator, such as the MSE or MAE, to evaluate the performance of our models. While these indicators can provide useful information about the accuracy of the models, they do not necessarily capture all aspects of model performance that are relevant in real-world financial applications. For instance, a model with low MSE or MAE may still be unsuitable for trading if it leads to unprofitable decisions.
Furthermore, the report only considers a single input dataset, namely the HSI index. However, it is well known that the behavior of the financial market is influenced by multiple factors, such as different interest rates, and the types of commodities etc.
Therefore, future studies should explore the use of multiple input dataset or variables to capture the complexity of the financial market. For example, adding different types of financial products such as futures, forex or bonds to be the input dataset can also be some good choices.
Future Studies
One possible avenue for future research is to investigate alternative deep learning models that can handle complex time-series data, such as Convolutional Neural Networks (CNNs) or Transformer models. These models have shown promising results in other domains, such as computer vision and natural language processing, and may provide new insights into the patterns of financial market data.
Another area for future research is to investigate the use of alternative performance metrics that capture other aspects of model performance that are relevant in financial applications. For instance, metrics such as the Sharpe ratio, the Sortino ratio, or the maximum drawdown can provide a more comprehensive evaluation of the model’s suitability for trading.
Moreover, future studies should also explore the use of multiple input variables to capture the complexity of the financial market. For instance, incorporating economic indicators, such as interest rates and inflation rates, may improve the accuracy of the model’s predictions and lead to more profitable trading decisions.
Finally, it is important to validate the performance of our models on out-of-sample data, that is, data that was not used in the training or testing phase. This will provide a more accurate estimate of the model’s generalization ability and its suitability for real-world financial applications.
Conclusion
In this report, we have compared the performance of three different time series forecasting models, including ARIMA, LSTM, and MLP, on the Hang Seng Index (HSI) dataset from 2010 to 2023. We have assessed the performance of these models using various evaluation metrics, such as RMSE, MAPE, MSE, and MAE.
The results showed that all three models could capture the overall trend of the HSI, but LSTM and MLP models outperformed the ARIMA model significantly. The LSTM and MLP models’ advantages lie in their ability to handle variable-length input sequences, capture long-term dependencies, and manage nonlinear interactions. Besides, MLP models can handle vast amounts of data, including category and numerical variables, making them helpful for capturing various input features that can impact stock prices.
However, it is crucial to recognize the models’ limitations and consider any outside factors that may affect financial market behavior. To create models that are more appropriate for real-world financial applications and capture the complexity of the financial market, future studies should explore the use of different input datasets or variables.
In conclusion, using LSTM and MLP models for time series forecasting can provide useful insights into market trends and prospective stock price movements. Investors can benefit from these models when combined with other analytical methods, as they can help make informed decisions and reduce risk.
Reference
Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.
Brownlee, J. (2018). Time series forecasting with Python: Discover the new way to analyze data and make predictions. Machine Learning Mastery.
Bengio, Y., Simard, P., & Frasconi, P. (1994). Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 5(2), 157-166. https://doi.org/10.1109/72.279181
Brownlee, J. (2020). How to Develop LSTM Models for Time Series Forecasting. Machine Learning Mastery. https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/ Chollet, F. (2018). Deep learning with Python. Manning Publications.
Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9(8), 1735-1780. https://doi.org/10.1162/neco.1997.9.8.1735
Lipton, Z. C., Berkowitz, J., & Elkan, C. (2015). A critical review of recurrent neural networks for sequence learning. arXiv preprint arXiv:1506.00019.
Patanè, G., & Maringhini, G. (2021). Stock Market Prediction Using Deep Learning Techniques: A Survey. Journal of Risk and Financial Management, 14(3), 107. https://doi.org/10.3390/jrfm14030107
Yao, L., & Deng, S. (2020). A comparative study on time series forecasting using deep learning approaches. Journal of Forecasting, 39(4), 606-618. https://doi.org/10.1002/for.2655
Code Appendix
ARIMA:
# Import necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
from pmdarima.arima import auto_arima
from sklearn.metrics import mean_squared_error
# Download and preprocess the data
hsi = yf.download('^HSI', start='2019-02-23', end='2023-03-23')
hsi = hsi['Close'].resample('M').mean() # Resample the data by month
# Split the data into training and test sets
train_data = hsi[:int(0.8 * len(hsi))]
test_data = hsi[int(0.8 * len(hsi)):]
# Fit the ARIMA model
model_autoARIMA = auto_arima(train_data, trace=True, suppress_warnings=True)
fitted = model_autoARIMA.fit(train_data)
# Make predictions
fc, conf_int = fitted.predict(n_periods=len(test_data), return_conf_int=True, alpha=0.05)
fc_series = pd.Series(fc, index=test_data.index)
lower_series = pd.Series(conf_int[:, 0], index=test_data.index)
upper_series = pd.Series(conf_int[:, 1], index=test_data.index)
# Plot the results
plt.figure(figsize=(12, 5), dpi=100)
plt.plot(train_data, label='Training')
plt.plot(test_data, color='blue', label='Actual HSI Price')
plt.plot(fc_series, color='orange', label='Predicted HSI Price')
plt.fill_between(lower_series.index, lower_series, upper_series, color='k', alpha=.100)
plt.title('HSI Price Prediction')
plt.xlabel('Time')
plt.ylabel('HSI Price')
plt.legend(loc='upper left', fontsize=8)
plt.show()
# Calculate performance metrics
rmse = np.sqrt(mean_squared_error(test_data, fc_series))
print(f'RMSE: {rmse:.2f}')
mape = np.mean(np.abs((test_data - fc_series) / test_data)) * 100
print(f'MAPE: {mape:.2f}%')
LSTM:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM, Dropout
# Load the data
df = pd.read_csv('HSI.csv')
df.set_index('Date', inplace=True)
# Visualize the closing price history
plt.figure(figsize=(16, 8))
plt.title('Close Price History')
plt.plot(df['Close'])
plt.xlabel('Date', fontsize=18)
plt.ylabel('Close Price USD ($)', fontsize=18)
plt.show()
# Create a new dataframe with only the 'Close' column
data = df.filter(['Close'])
# Convert the dataframe to a numpy array
dataset = data.values
# Get the number of rows to train the model on
training_data_len = int(np.ceil(len(dataset) * .95))
# Scale the data
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(dataset)
# Create the training data set
train_data = scaled_data[0:int(training_data_len), :]
x_train = []
y_train = []
for i in range(60, len(train_data)):
x_train.append(train_data[i-60:i, 0])
y_train.append(train_data[i, 0])
x_train, y_train = np.array(x_train), np.array(y_train)
# Reshape the data
x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
# Build the LSTM model
model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(x_train.shape[1], 1)))
model.add(LSTM(50, return_sequences=False))
model.add(Dense(25))
model.add(Dense(1))
# Compile the model
model.compile(optimizer='adam', loss='mean_squared_error')
# Train the model
model.fit(x_train, y_train, batch_size=1, epochs=1)
# Create the testing data set
test_data = scaled_data[training_data_len - 60:, :]
x_test = []
y_test = dataset[training_data_len:, :]
for i in range(60, len(test_data)):
x_test.append(test_data[i-60:i, 0])
# Convert the data to a numpy array
x_test = np.array(x_test)
# Reshape the data
x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], 1 ))
# Get the models predicted price values
predictions = model.predict(x_test)
predictions = scaler.inverse_transform(predictions)
# Get the root mean squared error (RMSE)
rmse = np.sqrt(np.mean(((predictions - y_test) ** 2)))
print('RMSE:', rmse)
# Plot the data
train = data[:training_data_len]
valid = data[training_data_len:]
valid['Predictions'] = predictions
# Visualize the data
plt.figure(figsize=(16,8))
plt.title('Model')
plt.xlabel('Date', fontsize=18)
plt.ylabel('Close Price USD ($)', fontsize=18)
plt.plot(train['Close'])
plt.plot(valid[['Close', 'Predictions']])
plt.legend(['Train', 'Val', 'Predictions'], loc='lower right')
plt.show()
MLP:
def MLP():
# Print title
print()
print(format('How to predict a timeseries using Multi Layer Perceptron in Keras', '*^92'))
# Import necessary libraries
import pandas as pd
import time
import numpy as np
from keras.layers.core import Dense, Dropout
from keras.models import Sequential
import matplotlib.pyplot as plt
# Start timer
start_time = time.time()
# Load the dataset
dataframe = pd.read_csv('/content/^HSI (4).csv', usecols=[1], engine='python', skipfooter=3)
dataframe.replace([np.inf, -np.inf], np.nan, inplace=True)
dataframe.dropna(inplace=True)
dataset = dataframe.values
dataset = dataset.astype('float32')
# Split into train and test sets
train_size = int(len(dataset) * 0.67)
train_dataset, test_dataset = dataset[0:train_size, :], dataset[train_size:len(dataset), :]
# Window -> X timestep back
step_back = 3
X_train, Y_train = [], []
for i in range(len(train_dataset) - step_back - 1):
a = train_dataset[i:(i + step_back), 0]
X_train.append(a)
Y_train.append(train_dataset[i + step_back, 0])
X_train = np.array(X_train)
Y_train = np.array(Y_train)
X_test, Y_test = [], []
for i in range(len(test_dataset) - step_back - 1):
a = test_dataset[i:(i + step_back), 0]
X_test.append(a)
Y_test.append(test_dataset[i + step_back, 0])
X_test = np.array(X_test)
Y_test = np.array(Y_test)
# Set up a MLP network in Keras
model = Sequential()
model.add(Dense(units=128, input_dim=step_back, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(units=64, input_dim=step_back, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(units=1, activation='linear'))
model.summary()
model.compile(loss='mean_squared_error', optimizer='rmsprop')
model.fit(X_train, Y_train, epochs=200, batch_size=2, verbose=1)
# Estimate model performance
print()
trainScore = model.evaluate(X_train, Y_train, verbose=1)
print('Train Score: %.2f MSE (%.2f RMSE)' % (trainScore, np.sqrt(trainScore)))
testScore = model.evaluate(X_test, Y_test, verbose=1)
print('Test Score: %.2f MSE (%.2f RMSE)' % (testScore, np.sqrt(testScore)))
# Evaluate the skill of the trained model
trainPredict = np.array(model.predict(X_train))
trainPredict = np.reshape(trainPredict, (len(trainPredict), 1))
testPredict = np.array(model.predict(X_test))
testPredict = np.reshape(testPredict, (len(testPredict), 1))
# Shift train predictions for plotting
trainPredictPlot = np.empty_like(dataset)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[step_back:len(trainPredict) + step_back, :] = trainPredict
# Shift test predictions for plotting
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(trainPredict) + (step_back * 2) + 1:len(dataset) - 1, :] = testPredict
# Plot baseline and predictions
plt.plot(dataset)
plt.plot(trainPredictPlot, label="True")
plt.plot(testPredictPlot, label="Prediction")
plt.ylabel('Stock price')
plt.legend()
plt.show()
# Print execution time
print()
print("Execution Time %s seconds: " % (time.time() - start_time))
MLP()
