This is an individual project of SDSC2004 – Data Visualization. I did the project in my year 1 2020/21 Semester B.
Project Requirement:
The Power Law degree distribution is an important finding in Network Science. Specifically, the Power Law says that in a real network, the distribution of nodes’ degrees roughly satisfies that ![]() , where
, where ![]() and
and ![]() are two parameters that may vary over different networks,
are two parameters that may vary over different networks, ![]() indicates a given degree and
indicates a given degree and ![]() denotes the percentage of nodes whose degrees are
denotes the percentage of nodes whose degrees are ![]() .
.
(1) Show that if ![]() ,
, ![]() has a linear relationship with
has a linear relationship with ![]() . (Hint: the linear relationship is
. (Hint: the linear relationship is ![]() , please find
, please find ![]() and
and ![]() . You need to figure out how to use c and
. You need to figure out how to use c and ![]() to represent
to represent ![]() and
and ![]() . The base of
. The base of ![]() and
and ![]() is e which means
is e which means ![]() ).
).
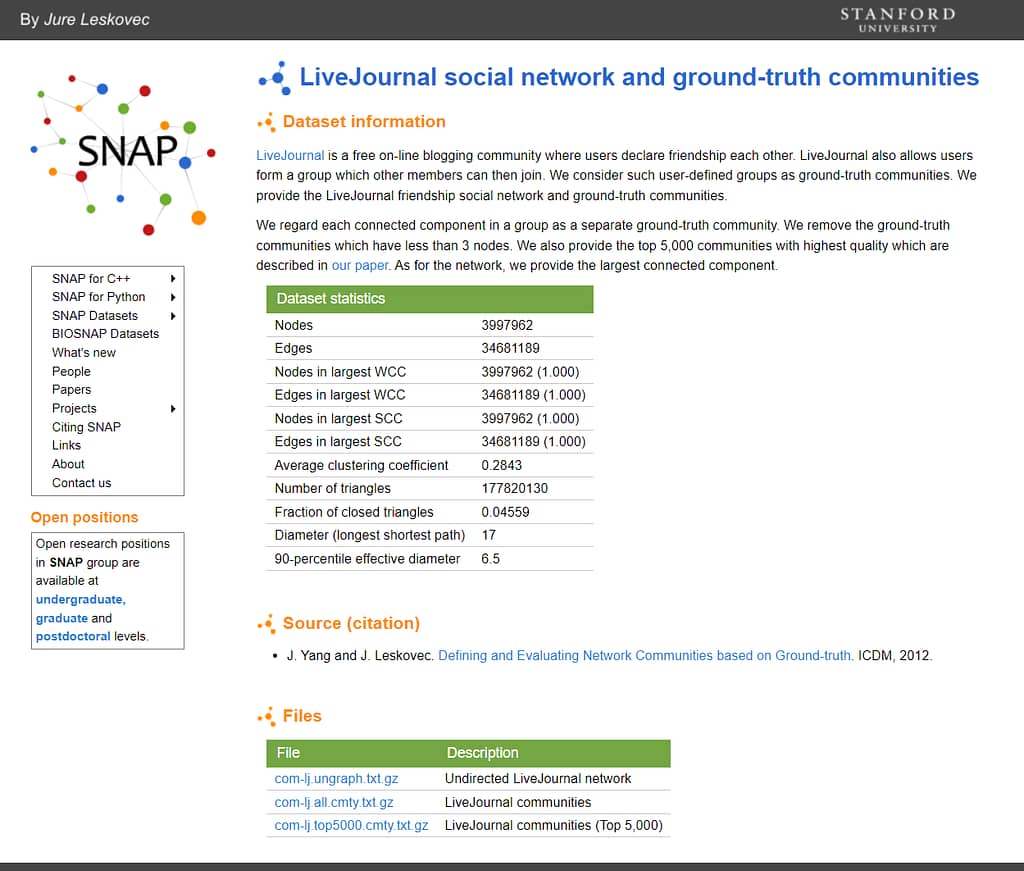
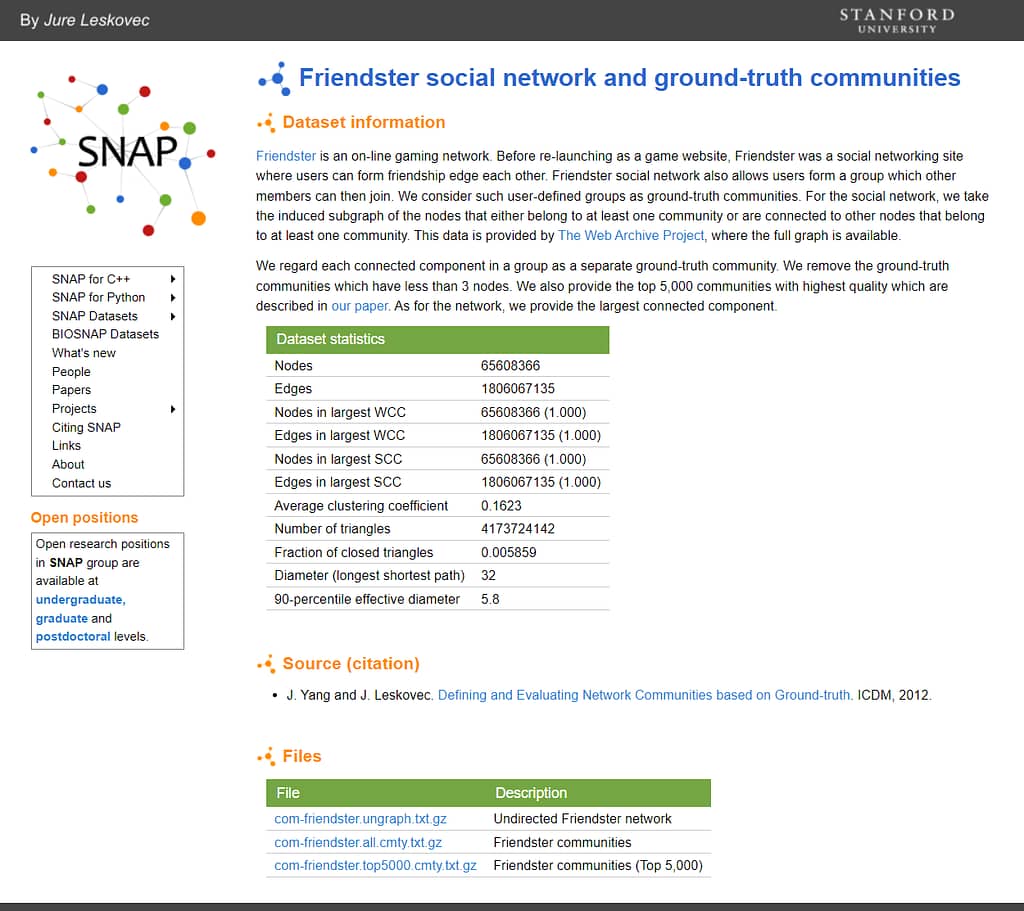
(2) Download the com-LiveJournal (https://snap.stanford.edu/data/com-LiveJournal.html) dataset and the com-Friendster (https://snap.stanford.edu/data/com-Friendster.html) dataset. Please download “Undirected XXXXXX network”. To verify if these two networks’ node degrees follow the Power Law, apply linear regression to fit the model ![]() . Report
. Report ![]() ,
, ![]() , and the R-Squared value for the two datasets.
, and the R-Squared value for the two datasets.
Below is my code (not perfect answer for sure):
import math
from scipy import stats
# Function to load data from a file
def load_data(filename):
# Open the file in read mode
file = open(filename, "r")
return file
# Function to map each node ID to its degree
def get_node_id_to_degree(file):
node_id_to_degree = {}
# Read the file lines, skipping the header if present
lines = file.readlines()[4:] # Adjust the number based on file header lines
for line in lines:
# Process lines with two integers representing nodes
if len(line.split()) == 2:
node1 = int(line.split()[0])
node2 = int(line.split()[1])
# Update the degree count for both nodes
add_to_dict(node1, node_id_to_degree)
add_to_dict(node2, node_id_to_degree)
return node_id_to_degree
# Helper function to update degree count in a dictionary
def add_to_dict(key, dictionary):
# Increment the node's degree count or add it if not present
if key in dictionary:
dictionary[key] += 1
else:
dictionary[key] = 1
# Function to map each degree to its frequency count
def get_degree_to_count(node_id_to_degree):
degree_to_count = {}
for node_id, degree in node_id_to_degree.items():
add_to_dict(degree, degree_to_count)
return degree_to_count
# Function to generate the x and y values for linear regression
def generate_xy(degree_to_count):
x = []
y = []
# Calculate the total number of nodes
number_of_nodes = sum(degree_to_count.values())
for degree, count in degree_to_count.items():
# Apply logarithmic transformation for the Power Law distribution
x.append(math.log(degree))
y.append(math.log(count / number_of_nodes))
return x, y
# Function to perform linear regression and return model parameters
def get_c1_c2_rsquared(x, y):
# Perform linear regression on log-log transformed data
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
return slope, intercept, r_value ** 2
# Main block to execute the functions
if __name__ == '__main__':
# Replace 'FileName.txt' with the actual file name
file = load_data("FileName.txt")
node_id_to_degree = get_node_id_to_degree(file)
degree_to_count = get_degree_to_count(node_id_to_degree)
x_list, y_list = generate_xy(degree_to_count)
c1, c2, rsquared = get_c1_c2_rsquared(x_list, y_list)
# Output the results
print(f"c1 (slope): {c1}")
print(f"c2 (intercept): {c2}")
print(f"R-squared value: {rsquared}")
Result: (cor. to 7 d.p.)
| c1 | c2 | R-Squared value | |
| com-LiveJournal | -2.3955318 | 2.5449043 | 0.9232843 |
| com-Friendster | -2.6347939 | 21.0607001 | 0.9194954 |
